平衡二叉树 Posted on 2021-06-17 00:00:00 2021-06-26 00:00:00 by Author 摘要 给定一颗二叉树,你能判断这颗二叉树是否是平衡二叉树吗?????? # 平衡二叉树 1. 题目描述 - 给定一个二叉树,判断它是否是高度平衡的二叉树。 - 本题中,一棵高度平衡二叉树定义为:一个二叉树*每个节点* 的左右两个子树的高度差的绝对值不超过 1 。 2. 示例描述 - 示例一 - 输入:[3,9,20,null,null,15,7] 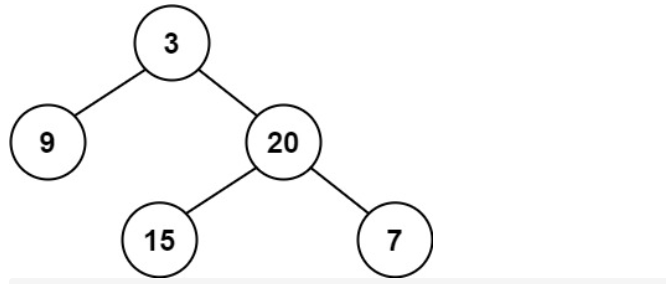 - 输出:true - 示例二 - 输入:[1,2,2,3,3,null,null,4,4] 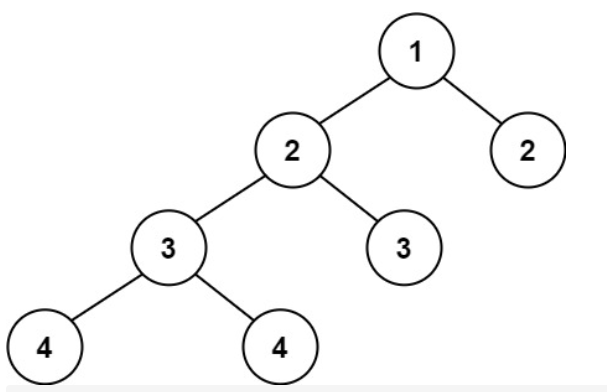 - 输出:false - 示例三 - 输入:[] - 输出:true 3. 解题思路 - 在拿到这道题目的时候,我觉得这道题目就是求二叉树深度的一个变型题目,只要找出每个节点的左右孩子节点的深度,然后判断该节点左右孩子节点最大深度差的绝对值是否小于2就行了,但是在实现的过程中,发现一个问题,就是假如一个节点左右孩子最大深度差的绝对值大于二的话,那么这颗二叉树整体就不是平衡二叉树,就不用继续遍历其他的节点,那么在遇到这种情况怎么提前结束尼,于是想了好久,还是木有想出来。最后还是借鉴Carl哥的题解才恍然大悟,我只能说,我太菜了,还得继续加油(可以关注代码随想录看Carl哥的题解)。 - 这里来讲讲我自己对他的题解的自我理解。首先我们考虑求每个节点左右孩子节点的最大深度用什么遍历尼。毫无疑问,肯定是后序遍历,那为什么要用后序遍历尼,我们可以这样理解,我们首先要找到该节点左右孩子节点的深度(这里的深度是指的是节点的最大深度),然后在对该节点进行处理,也就是判断该节点是否是平衡二叉树。以上步骤就是对二叉树进行左右中处理,是不是符合二叉树后序遍历的顺序尼,所以求每个节点左右孩子节点的最大深度用后序遍历,这点应该没有问题了吧。 - 然后考虑,假如一个节点不满足平衡二叉树的要求,那么整棵二叉树也就不是 平衡二叉树了,那么当遇到这种情况该怎么提前结束尼。这里Carl哥用的方法比较巧妙,即就是,在遍历该节点的时候,不管左孩子或者右孩子,如果他们不满足平衡二叉树的定义就直接返回一个负数(-1),如果左孩子与右孩子满足平衡二叉树的定义,那么再判断该节点是否满足平衡二叉树的要求(为什么这里还要判断该节点是否满足平衡二叉树的要求尼,因为我们知道该节点左右孩子是满足平衡二叉树的要求,但是你不知道左孩子与右孩子高度只差是否小于2,即你不知道以该节点为根节点的二叉树是否是平衡二叉树,所以最后还要判断以该节点为根节点的二叉树是否满足平衡二叉树的要求。),然后就这样一个一个节点的判断,如果全部节点满足平衡二叉树的定义,那么整棵二叉树就是一颗平衡二叉树,否则就不是。 - 以上理解属于自我的理解,有可能讲的有点不太清楚,那就先看看代码吧,说不定看完代码后就能理解了尼,具体代码如下。 4. 代码示例 ```java public boolean isBalanced(TreeNode root) { //如果根节点为空直接返回为true if (root == null) return true; //对每个节点进行判断是否满足平衡二叉树的定义 //如果没有一个节点违反平衡二叉树的定义,那么整棵二叉树就是一颗平衡二叉树 //如果其中一个节点违法平衡二叉树的定义,那么这棵树就不是一颗平衡二叉树 return depthRoot(root) == -1 ? false : true; } public int depthRoot(TreeNode node) { //如果该节点为空,那么其深度为0 if (node == null) return 0; //寻找该节点左孩子的深度 int leftDepth = depthRoot(node.left); //如果左孩子不是一颗平衡二叉树,就返回-1 //这里也就是找到一颗不满足的平衡二叉树定义要求的节点 //返回-1让其提前结束 if (leftDepth == -1) return -1; //寻找该节点右孩子的深度 int rightDepth = depthRoot(node.right); //如果右孩子不是一颗平衡二叉树,就返回-1 //这里也就是找到一颗不满足的平衡二叉树定义要求的节点 //返回-1让其提前结束 if (rightDepth == -1) return -1; //如果左右孩子都满足平衡二叉树的定义, //那么判断该节点是否是平衡二叉树 return Math.abs(leftDepth - rightDepth) > 1 ? -1 : 1 + Math.max(leftDepth, rightDepth); } ```
{{ item.content }}
{{ child.content }}