最大二叉树 Posted on 2021-06-23 00:00:00 2021-06-26 00:00:00 by Author 摘要 给一个数组,你能根据题目要求构造一颗最大二叉数吗?????? # 最大二叉树 1. 题目描述 - 给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下: 二叉树的根是数组 nums 中的最大元素。 左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。 右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。 返回有给定数组 nums 构建的 最大二叉树 。 2. 示例描述 - 示例一 - 输入:nums = [3,2,1,6,0,5] 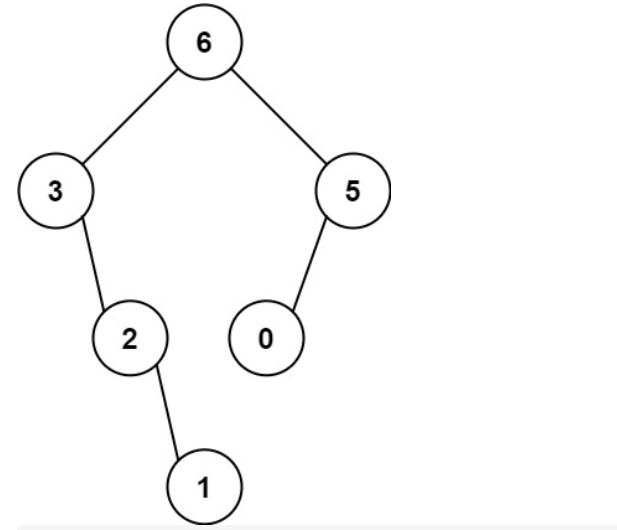 - 输出:[6,3,5,null,2,0,null,null,1] 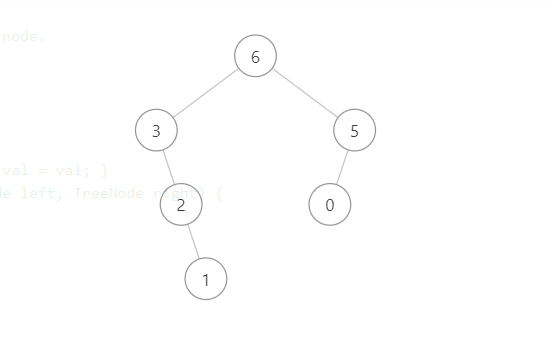 - 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。 - [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。 - 空数组,无子节点。 - [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。 - 空数组,无子节点。 - 只有一个元素,所以子节点是一个值为 1 的节点。 - [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。 - 只有一个元素,所以子节点是一个值为 0 的节点。 - 空数组,无子节点。 - 示例二 - 输入:nums = [3,2,1] <img src="http://e-blog.oss-cn-shanghai.aliyuncs.com/resources/user/getopsite/article/2021-06-23/-6187906083792081419.jpg" style="zoom:80%;" /> - 输出:[3,null,2,null,1] 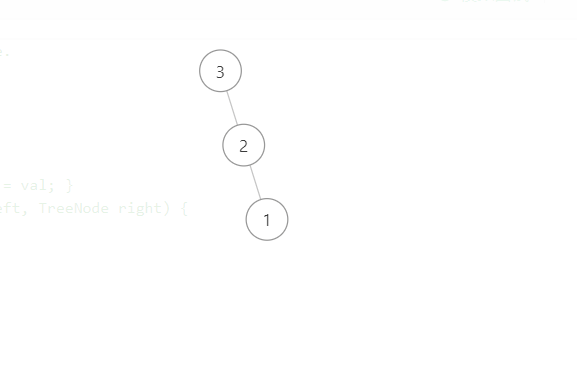 3. 解题思路 - 大家如果在看完本道题目的时候还是一脸困惑的话,那么建议去看看[中序与后序遍历构造二叉树](http://www.geticsen.cn/view/articles/detail/6e6ebd35-d8d3-46e5-a4d7-3e2c63b6cf92 "中序与后序遍历构造二叉树")这篇文章,只要理解与掌握了[中序与后序遍历构造二叉树](http://www.geticsen.cn/view/articles/detail/6e6ebd35-d8d3-46e5-a4d7-3e2c63b6cf92 "中序与后序遍历构造二叉树")这篇文章,然后解决本道题简直就是小菜一碟,只是在找父节点过程中发生了一些变化而已。 - 这里我在大概讲一下我遇到本题目的时候一些做法与个人理解。首先它给的题目比较长,让人看起来有点害怕,其实它讲的那么多,只是为了讲解清楚,怎么找`父节点`,然后找到了`父节点`,怎么去递归的问题。只要理解了上篇文章,那么当看完示例之后,就会明白题目的意思了。首先我们在给定的数组中找到一个最大值的位置,然后就构造一个节点,之后该位置的左边属于该节点的`左子树`,该节点位置的右边属于该节点的`右子树`,然后`左子树`与`右子树`的构造方式与该节点构造方式又是相同的,所以就再次用递归去做,那么递归的出口是什么尼,就是在递归过程中`左子树`或者`右子树`为空的条件下,跳出本次递归。直到构造完所有节点位置,那么本题就解决了。 - 具体代码如下,看完本题之后在和[中序与后序遍历构造二叉树](http://www.geticsen.cn/view/articles/detail/6e6ebd35-d8d3-46e5-a4d7-3e2c63b6cf92 "中序与后序遍历构造二叉树")这篇文章一起对比一下,会有意想不到的效果哟。不妨可以试试。 4. 代码示例 ```java public TreeNode constructMaximumBinaryTree(int[] nums) { //调用构造最大的二叉树的方法,该方法就是返回构造后的根节点 return constructMaxTree(nums, 0, nums.length - 1); } public TreeNode constructMaxTree(int[] nums, int left, int right) { //如果左子树或者右子树不为,说明还有节点需要构造 if (left <= right) { //从所给的数组中找出最大节点的位置,然后构造改节点 int maxPosition = findMaxNumber(nums, left, right); TreeNode node = new TreeNode(nums[maxPosition]); //之后构造该节点的左子树 //即该节点的左边位置就是该节点的左子树,即从本次递归时数组的起始位置,到该节点位置的左侧 node.left = constructMaxTree(nums, left, maxPosition - 1); //之后再构造该节点的右子树 //即该节点的右边位置就是该节点的右子树,即从到该节点位置的右侧,本次递归时数组的末尾位置 node.right = constructMaxTree(nums, maxPosition + 1, right); //最后返回该节点 return node; } //如果左子树或者右子树为空,说明该节点左侧或者右侧已经构造完成 return null; } //从所给的数组中找出最大值的位置,该方法比较简单 public int findMaxNumber(int[] nums, int left, int right) { int j = left; int temp = nums[j]; //从所给的起点位置到结束位置找出该位置之间的最大值,已经该最大值的位置 for (int i = left + 1; i <= right; i++) { if (temp < nums[i]) { temp = nums[i]; j = i; } } //返回最大值的位置 return j; } ```
{{ item.content }}
{{ child.content }}