对称二叉树 Posted on 2021-06-15 00:00:00 2021-06-26 00:00:00 by Author 摘要 给定一颗二叉树,你能判断这个二叉树是否是关于镜像对称尼??? # 对称二叉树 1. 题目描述 给定一个二叉树,检查它是否是镜像对称的。 2. 示例描述 - 示例 一 - 输入:[1,2,2,3,4,4,3,5,null,null,6,6,null,null,5]  - 输出:true - 示例二 - 输入:[1,2,2,3,4,4,3] 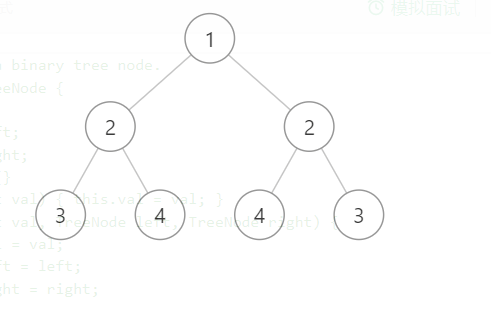 - 输出:true - 示例三 - 输入:[1,2,2,null,3,null,3] 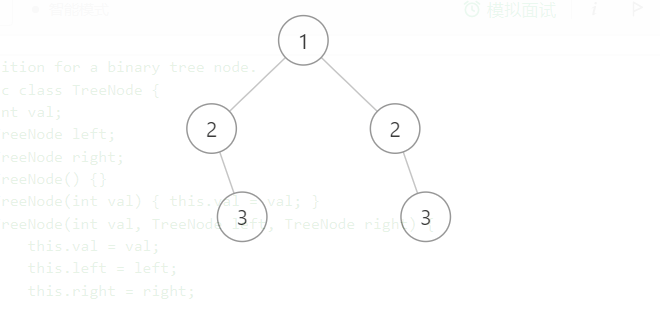 - 输出:false 3. 解题思路 - 这道题在leetcode上是一个简单的题,当我拿到这个题目的时候,我觉得这不是用层次遍历那个方法做吗,先层次遍历一下得到每一层的结果,然后每一层对半分,比较一下是否对称就可以了。于是我就动手做,但是有可能是我想的太美好了,当我提交代码的时候发现AC不通过,卡在`示例三`这个输入项上。我仔细看了一下,发现第三次有两个节点,并且值都是一样的,唯一不一样的就是不是镜像对称,然后我才明白,用层次遍历,只能找到每一次的节点,你不知道每个节点属于哪个父节点的左孩子,还是右孩子,所以就无法进行镜像对称比较,于是这条路行不通。 - 想了半天还是没有思路,于是就看了carl哥的这到题目的题解,讲的很通透。下面就来讲讲我自己看完题解后的个人理解。首先我们应该了解二叉树的镜像对称是什么。这里我们通过看示例应该明白,就是把一颗二叉树按照中位线折叠,对折后每个节点都有两个值相等的节点(根节点除外)。也就是一颗不为空的二叉树,如果有左孩子,那么必定要有右孩子,不然的话就不能形成镜像二叉树,如果没有右孩子,那么一定也没有左孩子,否则也不能构成一颗镜像二叉树。如果左孩子与右孩子都有,那么看左右孩子节点的值是否相等,如果不相等,那么也不能构成镜像二叉树。这以上就是判断镜像二叉树的条件,及就是递归的时候,递归出口的条件。如果一个节点既有左孩子,又有右孩子,那么如果镜像对称,就要比较`左孩子节点的左孩子`与`右孩子节点的右孩子`是否镜像对称,还有`左孩子节点的右孩子`与`右孩子节点的左孩子`是否镜像对称,如果这两个条件都满足,说明这个节点下的左右孩子这两颗二叉树是镜像对称的。这也是递归条件的入口。以上只是我个人的理解,具体代码示例如下。 4. 代码示例 ```java public boolean isSymmetric(TreeNode root) { //如果根节点为空,直接返回为true if (root == null) return true; //递归比较根节点的左孩子和右孩子是否对称 return compare(root.left, root.right); } //比较左右孩子是否对称 public boolean compare(TreeNode left, TreeNode right) { //如果左节点为空,右节点不为空,那么必不对称 if (left == null && right != null) return false; //如果左节点不为空,右节点为空,那么也必不对称 else if (right == null && left != null) return false; //如果左节点和右节点都为空,说明以及该节点的父节点下左右孩子节点对称的,返回true else if (right == null && left == null) return true; //如果左右节点都不为空,那么比较左右节点的值,是否相等,如果不相等,直接返回false else if (left.val != right.val) return false; //如果左节点右节点不为空,并且对应的值相等,那么就继续比较左右节点的孩子节点 //为什么要比较两次尼 //因为看是否对称,那么左节点的左孩子就要和右节点的右孩子比较 //左节点的右孩子就要和右节点的左孩子比较,如果该左右节点下的孩子节点对称,就返回true //否则就返回为false else return compare(left.left, right.right) && compare(left.right, right.left); } ```
{{ item.content }}
{{ child.content }}