二叉树的最近公共祖先 Posted on 2021-06-25 00:00:00 2021-06-26 00:00:00 by Author 摘要 给定一颗二叉树,并且给定二叉树上的两个节点,你能找出这两个节点的最近公共祖先吗????? # 二叉树的最近公共祖先 1. 题目描述 - 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。” 2. 示例描述 - 示例一 - 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 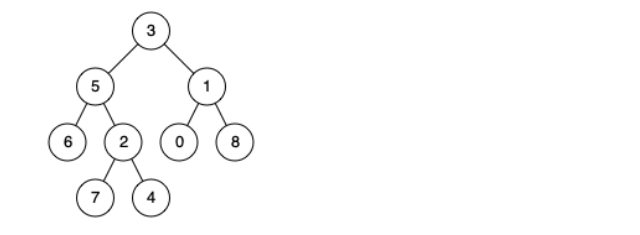 - 输出:3 - 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。 - 示例二 - 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 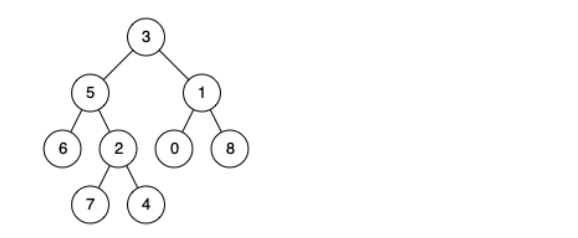 - 输出:5 - 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。 - 示例三 - 输入:root = [1,2], p = 1, q = 2 - 输出:1 3. 解题思路 - 这道题实现起来还是有点难度的,首先说一说我自己拿到这道题的错误的解法,并且从错误的解法中get到一个新的知识点。 - 对于涉及二叉树的问题大部分都是在遍历过程中解决的。那么首先确定应该用哪种形式去遍历二叉树。对于本道题来说,各位彦祖和亦菲先自己思考一下用什么遍历尼(到底是先序,中序还是后序尼)。思考好了吗??然后就要揭秘了:应该使用后序遍历。为什么用后序遍历尼,我当时的想法是这样的,因为题目要求要找最近的公共祖节点,我们都晓得不管用前中后序的哪一种形式的遍历(用递归方式实现时),都是有递归和回溯的思想在里面的。我们在需要判断二叉树所有的节点是否是所给的两个节点的祖父节点,并且找到最近的父节点,这就需要我们从下到上的去遍历整棵二叉树,因为从下到上去遍历二叉树的时候,每到一个节点,他的孩子节点以及遍历过了,那么我们再判断该节点是否是这两个所给节点的父节点,只要该节点是这两个节点的父节点并且是第一次那么就说明找到了公共节点,并且是最近的公共节点。所以需要从下到上的遍历整棵二叉树,而后序遍历就是属于从下到上的遍历思想,那么这道题就需要使用后序遍历了。 - 我们知道遍历了方式,那么我们再去处理怎么找到最近公共祖先的逻辑就可以了。下面是我当时自己的实现方式(其实是错的,我记录下来,就是让大家一起想想为什么错了,之后再理解正确的解法,就会得到新的感受),这里的逻辑是这样的,我首先定义两个全局标志位和一个全局父节点的结果变量,两个全局标志位一个标志是判断节点p在正在遍历的节点之下是否在后序中被访问到,另一个标志位是判断节点q在正在遍历的节点之下是否在后序遍历中被访问到。如果都被访问到,那么就返回正在遍历的节点,找到了结果。具体代码见代码一(错误实现代码!!) - 当时我以为这道题就这样解决了,然鹅我在LeetCode上提交代码的时候,发现AC不通过,一共31个测试用例,通过了18个,并且卡在一个测试用例中,具体情景如下。 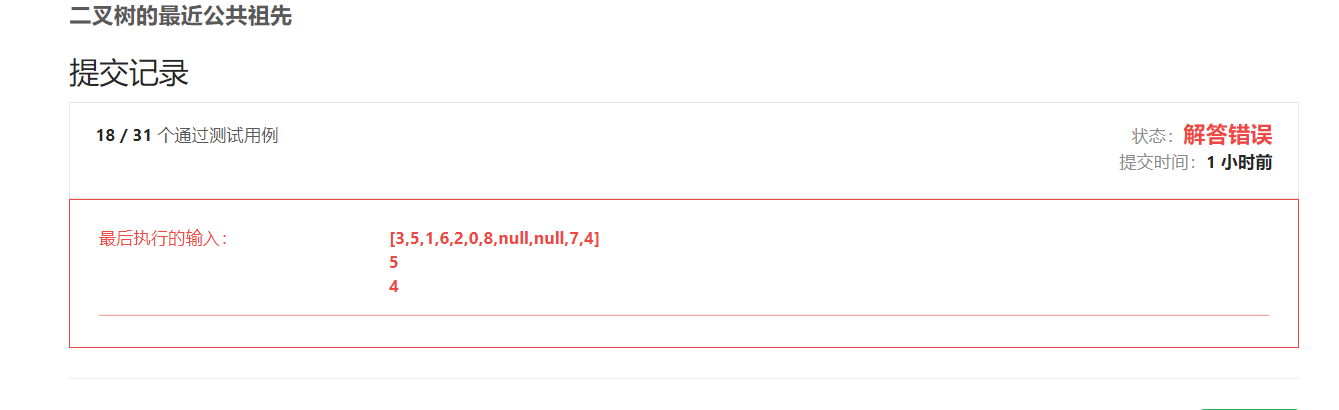 - 当时我又检查了一遍,并且再次拿测试用例自己画出二叉树的树形结构,自己亲自动手走了一遍,发现也没有问题啊,但是就是AC不通过啊,当时就非常百思不得其解,然后就看了看代码随想录Carl哥写的题解,不看不知道,一看发现自己对递归与回溯的实现思想还是理解的不够到位。 - 在我仔细理解了他的思想与实现方式的时候。我发现了自己的问题,我的逻辑是假如两个节点都被访问到然后直接返回该节点,该节点就是最终的节点,但是实际上并不是这样的,因为这是在递归与回溯中返回,并不是直接结束该函数的调用,而是返回到上次调用该函数的调用点处。本次返回至少本次递归时候的返回,并不代表整个递归函数的返回,所以这里实现的逻辑还是有问题的。这是我再次对递归与回溯思想的理解。 - 之后我再次看看了题解,发现对于二叉树的递归与回溯的形式,原来有两种返回的方式,我自己的理解是:第一种就是不需要遍历整棵二叉树,即就是在遍历过程中满足题目要求就返回。第二种就是遍历完整棵二叉树之后才能得到最终结果,所以在动手做二叉树题目的时候这点也需要考虑进去。 - 那么怎么在遍历过程中,发现满足最终结果就返回尼(也就是第一种情况),这需要在定义递归与回溯函数的时候,需要有返回值的形式。我们之前在用递归形式遍历二叉树的时候一般在固定位置写逻辑代码。比如在中序遍历的时候就是在调用递归函数进入左孩子递归函数之后,调用右孩子递归函数之前进行写逻辑代码。在后序遍历的时候就是在遍历右孩子递归函数之后写逻辑代码。然鹅这种形式是属于遍历整棵二叉树时候的写法。不适合第一种形式,第一种形式写法,就是在每一次调用递归函数的时候需要得到一个返回值,这个返回值如果满足条件的时候就返回,那么在下次调用的时候,这个返回值已经满足条件了,那么下次调用的时候也是返回 上次的返回值,那么直到最后的结果就是第一个找到的返回值,那么我们在找到结果后就返回,和遍历完成后得到的值是第一次返回的结果值是一样的,那么这就是第一种情况的形式了。我在看完题解之后个人理解就是这样的。有可能自己讲的还是不太清楚,大家可以去Carl哥的公众号去看看,在深入理解一下,下面是我自己错误的代码和已经可以AC通过的代码,大家可以看看比较之后再次理解。 4. 代码示例 ```java 代码一(未能全部AC): //判断所给节点的第一个节点的标志位 boolean pFlag = false; //判断所给节点的第二个节点的标志位 boolean qFlag = false; //最后结果,即为最近公共节点的遍历 TreeNode result = null; public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if(root!=null){ //后序遍历的形式 lowestCommonAncestor(root.left,p,q); lowestCommonAncestor(root.right,p,q); //如果遍历的节点是p节点 if(root == p){ //该节点被访问过了 pFlag = true; } //如果遍历的节点是q节点 if(root==q){ //该节点被访问过了 qFlag = true; } //如果两个节点都被访问了 if(pFlag&&qFlag){ result = root; //返回最终结果(就是这里有问题) return result; } } //返回最终结果 return result; } ``` ```java 代码二(正确的形式) public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { //如果其中一共节点被访问到了,那说明找到一共节点是公共节点 if (root == q || root == p || root == null) return root; //该节点下左子树寻找公共节点的值 TreeNode left = lowestCommonAncestor(root.left, p, q); //该节点右子树寻找公共节点的值 TreeNode right = lowestCommonAncestor(root.right, p, q); //如果左子树节点值与右子树节点值都不为空,那说明该节点是最近公共祖父节点 if (left != null && right != null) return root; //左子树为空,那么右子树返回的值为公共祖父节点 if (left == null && right != null) return right; //否则就是左子树节点的值 else if (left != null && right == null) return left; //左子树与右子树的值为空,那么就返回为空 else { return null; } ```
{{ item.content }}
{{ child.content }}