找出左下角的值 Posted on 2021-06-20 00:00:00 2021-06-26 00:00:00 by Author 摘要 给定一个二叉树,在树的最后一行找到最左边的值,你能找出来吗??????? # 找出左下角的值 1. 题目描述 - 给定一个二叉树,在树的最后一行找到最左边的值。**注意:** 您可以假设树(即给定的根节点)不为 **NULL**。 2. 示例描述 - 示例一 - 输入:[1,null,2,null,null,3,null] 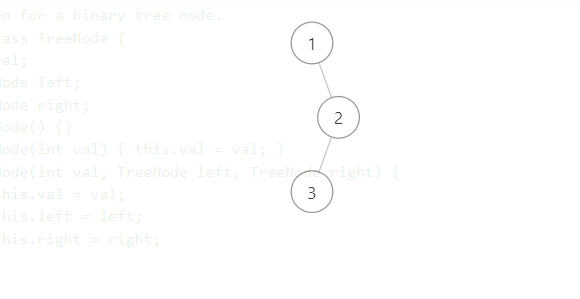 - 输出:3 - 解释:二叉树最后一层,只有一个节点3,3那么就是最终结果。 - 示例二 - 输入:[1,null,2,3,6,7,8,9,null] 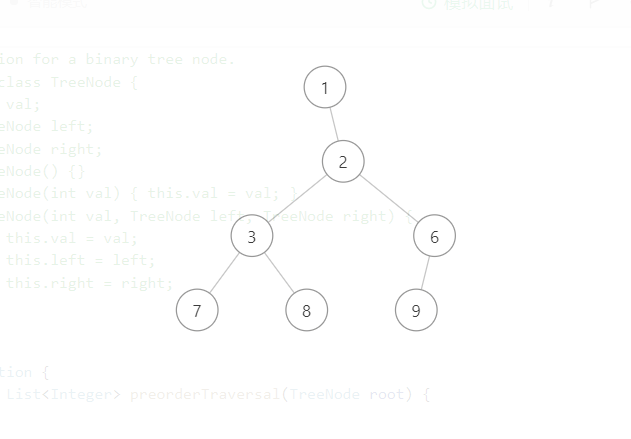 - 输出:7 - 解释:二叉树最后一层有3个节点,最左下角的是7。 3. 解题思路 - 其实这道题和前面讲的一道`左叶子之和`的题目非常类似,简单来说,就是那道题的变型。为什么这么说尼,因为那道题的做法完全可以套在本题中,只是本题在此基础上变动一下就能解决本题。大家可以看完[左叶子之和](http://www.geticsen.cn/view/articles/detail/ca5d43b8-f895-4ff0-b1b8-f60b4fdbad2d "左叶子之和"),再看这篇文章,就能恍然大悟了。 - 接下来,我们分析这道题目,首先我们知道,给一个二叉树,一般都会涉及遍历二叉树,但是遍历二叉树有左中右三种遍历方式,那应该选那种遍历方式尼,这需要根据每到题目的解题思路而言,这里我采用前序遍历,因为这里说了找最后一层最左侧的节点,那么前序遍历符合本题的要求。接下来还要考虑一个问题,就是找出最后一层,那么最后一层就是深度最大的一层,此时也涉及到求二叉树高度的这道题目,大家可以看看[二叉树最大深度](http://www.geticsen.cn/view/articles/detail/7e86801f-699c-48c9-9aae-ca89f752ef3e "二叉树最大深度")这篇文章。我们只要到达下一层,那么这一层的第一个节点就是我们想要的节点,这层其余的节点都是陪衬,因为我们要找出最左侧的节点,所以只需要每一个前序遍历的第一个节点,然后再根据深度遍历,如果本层的深度大于之前节点的深度,那么本层的第一个节点记录再最终结果中,同时找一个存储本层第一个节点的深度变量,把本层的深度暂存起来,直到找到二叉树最后一层的第一个节点,那么最终结果就找到了,此时就已经完成了本题目,如果大家理解`二叉树最大深度`和`左叶子之和`两篇文章,那么这道题实现起来挺简单的,下面是本题的实现代码。 4. 代码示例 ```java //存储最终的结果的变量 int result = 0; //存储最终结果的深度变量 int deep = 0; public int findBottomLeftValue(TreeNode root) { //因为深度为0的时候,根节点的值就是最终结果 result = root.val; //先序变量找出最终结果 recursion(root, 0); return result; } public void recursion(TreeNode root, int tempDeep) { //以下是先序遍历和求二叉树最大深度结合的一般写法,只是在此基础上变化了一下 if (root != null) { //如果是叶子节点 if (root.left == null && root.right == null) { //到达新的一层,那么第一个节点就是要找的节点, //此时结果存放第一个节点的值,深度遍历存储这个节点的深度 //从哪里体现出每一层的第一个节点尼 //从tempDeep > deep (没有等于),那么这一层的其余节点和第一个节点深度是一样的 //所以遍历到这层的其余节点,就进不去这个判断,这就达到找到该层第一个节点 //也就是每层最左侧的一个节点 if (tempDeep > deep) { result = root.val; deep = tempDeep; } } //先序遍历与求二叉树的最大深度结合的一般写法 recursion(root.left, tempDeep + 1); recursion(root.right, tempDeep + 1); } } ```
{{ item.content }}
{{ child.content }}